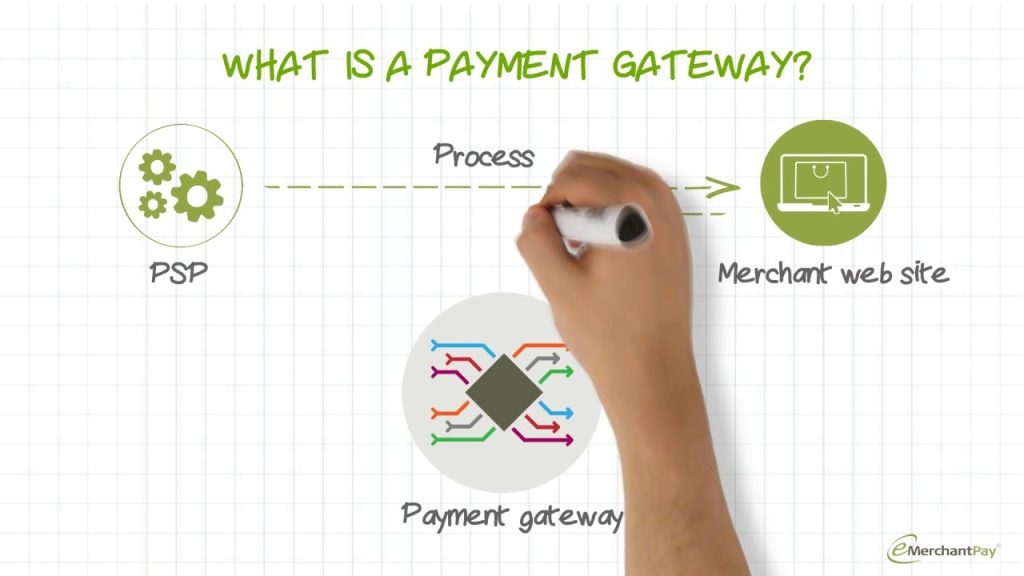
Packaging dimensions are crucial for shipping and storage, but the terms “length,” “width,” “height,” and “depth” can be ambiguous. To avoid confusion, always clarify which measurement corresponds to which side of the box. For example, length is often the longest side, width the shorter side, and height the vertical dimension. However, this isn’t universally standardized. Some companies might use different conventions, leading to errors in order fulfillment and warehousing. Precise measurements are essential to prevent issues with carriers like UPS, FedEx, or USPS, who have specific size and weight restrictions affecting shipping costs and delivery times. Accurate dimensions are also vital for fitting packages onto pallets efficiently, optimizing storage space and reducing transportation expenses. Ignoring this can result in wasted space, higher shipping bills, and increased risk of damage during transit. Always refer to clear diagrams provided by the manufacturer or retailer to ensure accurate measurement interpretation.
What are the four kinematics equations?
As a regular user of these equations, I’ve found these four kinematics equations invaluable: v = v₀ + at; Δx = (v + v₀)/2 * t; Δx = v₀t + (1/2)at²; v² = v₀² + 2aΔx. They’re essential for solving any constant-acceleration motion problem. Remember, these equations assume constant acceleration. It’s crucial to correctly identify your knowns and unknowns before selecting the appropriate equation. For example, if you know initial velocity, acceleration, and time and need to find displacement, the third equation is your best bet. If you lack time information, but know initial and final velocities and acceleration, the fourth equation is more efficient. Master these and you’ll be conquering physics problems in no time!
What is L * B * H in maths?
OMG! L * B * H? That’s the secret formula to calculate the volume of a cuboid! Think of it like this: you’re buying a super cute storage box (a cuboid, duh!), and you need to know how much stuff you can cram inside. L is the length – how long the box is. B is the breadth – how wide it is. And H is the height – how tall it is. Multiply them all together (L * B * H), and *bam*! You get the volume (V = lbh) in cubic units! So before you buy that adorable new storage ottoman, use this formula to make sure it’s BIG enough for all your amazing new shoes!
Pro Tip: Remember to use consistent units (inches, centimeters, etc.) for all three measurements to get an accurate volume. Otherwise, you might end up with a storage box that’s way too small (or way too big!) for your fabulously trendy collection.
What does m * g * H mean?
Ever wondered what that mgh equation means? It’s the secret sauce behind potential energy calculations, specifically for gravity’s pull. Think of it as the energy an object possesses *because* of its position in a gravitational field.
Unpacking the Formula:
- m (mass): The object’s mass in kilograms. A heavier object naturally has more potential energy at the same height.
- g (acceleration due to gravity): This is approximately 9.8 m/s² on Earth. It represents how forcefully gravity pulls the object downwards. Note that ‘g’ varies slightly depending on location; it’s slightly less at higher altitudes and slightly more at lower altitudes.
- h (height): The object’s height above a chosen reference point, usually the ground, measured in meters. The higher the object, the greater its potential energy.
Real-World Applications: Understanding potential energy (PE = mgh) is crucial in various fields:
- Civil Engineering: Designing dams, bridges, and buildings requires precise calculations of potential energy to ensure stability and safety.
- Mechanical Engineering: Analyzing the operation of hydraulic systems, roller coasters, and other machines that leverage gravitational potential energy.
- Physics: Fundamental to understanding concepts like energy conservation, where potential energy can be converted into kinetic energy (energy of motion).
Beyond Earth: While 9.8 m/s² works well on Earth, remember that ‘g’ changes on other celestial bodies. On the Moon, for example, ‘g’ is significantly lower, meaning an object at the same height would have less potential energy.
What is n * m equal to?
So you’re wondering what n * m equals? It depends on the units! Think of it like shopping – you need the right units to compare apples to apples (or, in this case, Newtons to pounds).
Newton-meters (N⋅m) are the standard unit for torque or moment of force in the SI system. One N⋅m is roughly 0.74 pound-force-feet. Perfect for those DIY projects!
Pound-force-feet (lb⋅ft) is a common unit in imperial units. If you’re working with older tools or instructions, you’ll likely see this. One lb⋅ft is about 1.36 N⋅m.
Smaller units exist too. An ounce-inch (oz⋅in) is handy for smaller applications. It’s approximately 7.06 millinewton-meters (mN⋅m). Great for those intricate model kits!
For the scientifically minded: A dyne-centimeter (dyn⋅cm) is a tiny unit, equal to 10-7 N⋅m.
Bottom line: Always double-check your units before making calculations or comparing values. A simple conversion error can make a big difference!
What is w * d * h?
W * D * H, or Width times Depth times Height, is a formula I use constantly. It’s crucial for everything from calculating the cubic footage of my new storage unit (to make sure my latest online furniture haul fits!) to figuring out how much topsoil I need for my garden. Remembering that width, depth, and height need to be in the *same* units (inches, feet, meters, etc.) is key – otherwise, your calculations will be way off. For irregular shapes, it gets trickier, of course, often requiring breaking the shape into smaller, more manageable rectangular prisms and calculating each separately. Pro-tip: many online calculators handle this, saving you a headache. Also, don’t forget to account for packaging dimensions when buying online – that extra few inches can make a big difference!
Is LXWXH the correct order?
OMG, yes! LXWXH is totally the correct order for dimensions! It’s like, the most important thing to know when you’re shopping online for that amazing new [insert desired item here], especially furniture! You absolutely need to get the measurements right, or that gorgeous new sofa won’t fit through the darn doorway!
Length is always the longest side, think how long it stretches out. Then comes width, which is the measurement across – you know, how wide it is? And finally, height, which tells you how tall it is. So always check those numbers carefully. I learned that the hard way with that ridiculously huge mirror!
Pro tip: Before buying anything bulky, measure your space twice! Seriously, I cannot stress this enough. It’s saved me from so many returns and a lot of frustration. Plus, knowing the dimensions lets you compare similar items easily and ensures that your new purchase is the *perfect* fit for your home. And that’s what we all want, right? A perfectly sized, gorgeous new addition that doesn’t cause a logistical nightmare!
Is it W * H or H * W?
The question of whether to use W * H or H * W for image dimensions is surprisingly significant. The graphics industry standard, and the method used by virtually all image editing software and file formats, is width × height. This convention stems from the perspective of the viewer; you describe the image as it appears to you, starting with the horizontal extent (width) and then the vertical (height).
Thinking about this in terms of a digital canvas helps. You’re essentially describing the horizontal and then the vertical number of pixels. This consistency is crucial for seamless integration across different platforms and software. Using the incorrect order can lead to misinterpretations, especially in professional settings where precise dimensions are paramount. Conversely, adhering to the width × height standard ensures clear and unambiguous communication.
While some niche applications or older systems might deviate, adopting the W × H convention avoids confusion and guarantees your specifications are universally understood. It’s a simple yet essential aspect of digital image handling that ensures professional results.
What is the 5 formula of kinematics?
The commonly cited “fifth kinematic equation,” Δx = (v + v₀)/2 * t, isn’t fundamentally distinct from the other four; it’s derived from them. It’s a useful shortcut, however, for calculating displacement when you know the average velocity [(v + v₀)/2] and the time elapsed. This equation bypasses the need to solve for acceleration first, streamlining calculations. This is particularly handy in scenarios where acceleration is either constant or irrelevant to the problem at hand, such as calculating the distance traveled by a car during a specific timeframe given its initial and final speeds.
While practical, remember that this equation’s applicability is limited to situations with constant acceleration. For scenarios involving variable acceleration, calculus-based methods become necessary. This equation provides a concise solution for many everyday kinematics problems involving uniform motion, making it a valuable tool in a physicist’s arsenal.
Understanding the relationships between all five kinematic equations is key. While this equation provides a direct path to displacement, others offer insight into acceleration or final velocity, providing flexibility depending on the known parameters of a given problem. Choosing the right equation directly impacts the efficiency of your solution.
What does L * C mean?
L*C*h is a color representation where L* denotes lightness, a perceptual measure of how light or dark a color appears. It’s independent of hue and chroma, unlike older systems. C*, chroma, signifies color saturation – how vivid or intense the color is. A higher C* means a more saturated color. Think of it like the “punch” of the color. Low C* values result in desaturated, pastel-like shades. Finally, h, the hue angle, represents the pure color; it’s what we typically think of as red, green, blue, etc., expressed as a degree on a color wheel (0° is red, 120° is green, 240° is blue). These values are derived from the a* and b* coordinates of the L*a*b* color space, a much more perceptually uniform system than RGB or CMYK, making color comparisons and adjustments far more accurate and reliable, especially for applications like professional color matching and printing. I consistently get superior results with this system for my favorite home improvement projects because of this increased accuracy!
What are the 4 basic quantities of kinematics?
Kinematics is like shopping for the perfect outfit – you need the right components! There are actually five basic quantities, not four, to fully describe motion: displacement (think of it as the distance and direction from your starting point to your ending point – like navigating from the online store to your house!), initial velocity (your starting speed at t=0; it’s like how quickly you clicked “add to cart”), final velocity (your speed when you arrive – imagine how fast the delivery truck is going!), acceleration (how quickly your speed changes – a sudden sale might make you accelerate your purchasing!), and time (how long the whole process takes – shipping times are important!). Initial velocity specifically describes the speed at the very beginning, t=0, like when the item is first listed.
Understanding these five quantities is crucial to analyzing motion, just like understanding product descriptions, reviews, and shipping information is vital for successful online shopping. Each quantity plays a critical role in calculating others. For example, knowing your initial and final velocity and the time allows you to calculate your acceleration! (A killer deal makes you accelerate your purchasing!)
Is it H * W or W * H?
The question of “H * W or W * H?” is a surprisingly common one, especially when dealing with screen resolutions or image dimensions. The graphics industry standard is unequivocally width × height. Think of it like this: you’re describing the dimensions from your perspective, starting with the horizontal span (width) and then the vertical (height).
This convention isn’t arbitrary; it’s consistent with how we naturally perceive and describe objects. We tend to note the horizontal extent before the vertical. Imagine describing a room: you’d likely say “it’s 10 feet wide by 12 feet long,” not “12 feet long by 10 feet wide.” The same principle applies to digital images and screen resolutions.
Understanding this is crucial for several reasons. Incorrectly specifying dimensions can lead to mismatched aspect ratios when scaling images, resulting in distorted visuals. Furthermore, many software applications and APIs rely on this standard, so using the wrong order can cause compatibility issues and unexpected behaviors. For instance, when configuring a game’s resolution, using the wrong order could lead to unexpected stretching or compression of the game’s visuals.
Beyond image dimensions and screen resolutions, this width × height convention often extends to other aspects of gadget specifications. For example, when discussing the size of a phone screen, the manufacturer will typically list the width before the height. Paying attention to this detail ensures that you understand the actual dimensions of your device or media.
In short, remember: width × height. It’s the industry standard, it’s intuitive, and it prevents a world of potential headaches.
What is m * g equal to?
m * g, or mass times acceleration due to gravity (g ≈ 9.8 m/s² on Earth), calculates an object’s weight. Weight, unlike mass, isn’t inherent; it’s the force exerted on an object by gravity. This means your weight would change on the moon, where ‘g’ is significantly lower, even though your mass remains the same. Think of it like this: mass is the amount of “stuff” in an object, while weight is how strongly that “stuff” is pulled downwards. The result, expressed in Newtons (N), is a crucial factor in numerous applications, from structural engineering (calculating load-bearing capacity) to designing safe and effective spaceships. Understanding this simple equation is fundamental to comprehending forces in our everyday world. The weight of an object is directly proportional to its mass; double the mass, double the weight (at the same gravitational pull). Conversely, a decrease in gravitational acceleration leads to a proportionate decrease in weight.
What is M * G * H in physics?
Looking for the meaning of M * G * H in physics? It’s the formula for potential energy due to gravity! Think of it like this: you’re shopping online and adding items to your cart. Each item has a certain “potential” to give you satisfaction (or, you know, deliciousness). Similarly, an object held at a height has potential energy.
The formula, P.E. = mgh, breaks down like this:
- m (mass): This is like the weight of your online shopping cart – the heavier it is (more items), the more “potential energy” (cost!) it has.
- g (acceleration due to gravity): This is a constant (approximately 9.8 m/s² on Earth). It’s like the fixed shipping cost. It doesn’t change based on what you buy (unless you’re buying something super heavy and needing special delivery).
- h (height): This is how high the object is lifted. In online shopping terms, think of this like how much “prestige” a product has – a limited edition item has more “potential” if it’s more difficult to get.
So, the higher you lift an object (increase ‘h’), the more potential energy it gains. The heavier the object (increase ‘m’), the more potential energy it also gains. This potential energy can be converted into kinetic energy (movement) if you let the object fall.
Bonus fact: While 9.8 m/s² is a good approximation for ‘g’ near Earth’s surface, this value actually varies slightly depending on your location. The further you are from the Earth’s center, the weaker the gravitational pull and the smaller the value of ‘g’.
- Higher altitudes mean lower ‘g’.
- Different planets have different values for ‘g’. For example, the moon’s gravitational pull is much less strong than Earth’s
What is l * c * h color space?
As a regular buyer of produce, I find the CIE L*C*h color space incredibly useful for assessing ripeness. It’s essentially a tweaked version of the L*a*b* color space, presented as a vector. The key is the hue angle (h); it’s a fantastic indicator of how ripe something is.
Think about tomatoes: their color change from green to red is perfectly reflected in the hue angle. It shifts from roughly 180° (green) towards 0° (red). This isn’t just about tomatoes, though. Many fruits and vegetables exhibit similar shifts in hue as they ripen. Understanding this helps me choose the best produce.
Here’s what I’ve learned to look for:
- L* (Lightness): Higher values mean brighter colors. A slightly lower L* value might indicate a more concentrated color, suggesting ripeness in some cases.
- C* (Chroma): This represents color saturation or intensity. A higher C* generally means a more vibrant color and, often, better ripeness (though not always).
- h (Hue Angle): As mentioned, this is the crucial part. It’s the direction of the color on a color wheel. The change in hue angle is the best indicator for the ripening process.
Knowing how the hue angle changes for specific produce is a game-changer for selecting optimally ripe items. For example:
- Bananas: The hue shifts towards yellow as they ripen.
- Avocados: The hue might darken slightly as they transition to being ready to eat.
- Mangoes: The hue changes towards more reddish or yellow tones depending on the variety, indicating ripeness.
While the exact hue angle for optimal ripeness varies greatly between fruits and vegetables, monitoring the change in this parameter is always valuable.
What is the CIE XYZ and xyY color space?
CIE XYZ and xyY are fundamental color spaces in the world of color science. CIE XYZ, the parent space, is a three-dimensional representation encompassing all perceivable colors, with X, Y, and Z representing the tristimulus values. These values are not directly intuitive, but they form the basis for many other color spaces.
The xyY color space cleverly simplifies XYZ. It retains the Y value, representing luminance or brightness. The ‘xy’ components are derived from XYZ and represent chromaticity – essentially, the color’s hue and saturation, independent of brightness. This allows for a two-dimensional representation on the famous xy chromaticity diagram. This diagram is invaluable for visualizing the gamut of a particular device (like a monitor or printer) and comparing color spaces. You’ll often see it used to show the range of colors reproducible by a specific technology.
Think of it this way: XYZ gives you the full recipe for a color, including its brightness. xyY gives you the color recipe without the brightness, allowing for easier comparison of hues and saturations across different brightness levels. It’s a crucial tool for color professionals in fields like graphic design, photography, and manufacturing.
While XYZ provides a complete color specification, xyY’s reduced dimensionality makes it incredibly useful for quick visual assessments and comparisons of colors. Its widespread adoption underlines its importance in standardizing and understanding color reproduction.