What are the different types of logic gates?

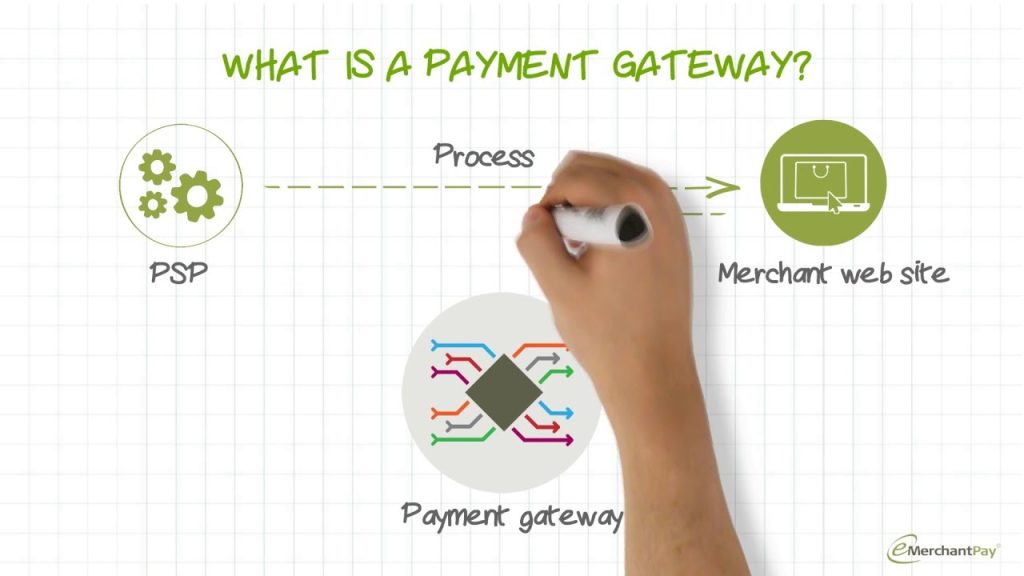
Logical elements, the fundamental building blocks of digital circuits, come in a surprising variety of physical implementations. Beyond the common electronic versions using diodes and transistors, consider the fascinating history and diverse applications of other technologies. Mechanical implementations, while slower and bulkier, offer a tangible demonstration of Boolean logic principles. Electromechanical relays, a crucial stepping stone in computing’s early days, leveraged electromagnetism for switching, highlighting the transition from purely mechanical systems. Pneumatic and hydraulic systems, using air pressure and liquid flow respectively, represent less common but equally valid approaches, finding niche applications where robustness or specific environmental conditions are paramount. Optical implementations, using light signals for logic operations, are gaining traction, promising faster speeds and lower energy consumption in cutting-edge applications. The choice of implementation depends on factors such as speed, power consumption, reliability, cost, and the specific application requirements. For instance, while electronic implementations dominate modern digital systems due to their speed and miniaturization potential, mechanical or optical solutions may prove superior in specific contexts demanding extreme robustness or high-bandwidth signal transmission. Each technology offers a unique trade-off between performance and practical considerations, showcasing the remarkable adaptability of logic element design.

What are the fundamental elements of logic?

Logic’s core components are premises and conclusions. These form the building blocks of inferences and arguments, acting as the fundamental units of logical analysis. Think of premises as the raw materials, the evidence or assumptions that support a claim. The conclusion is the claim itself – the point you are trying to prove. A valid argument, like a well-designed product, demonstrates a clear, irrefutable link between premises and conclusion; the conclusion logically follows from the premises. This relationship can be tested through various methods, much like we rigorously test product functionality, to determine whether the argument holds water. For example, invalid arguments suffer from flaws analogous to product defects – they might contain hidden assumptions (like undocumented features), or their reasoning might be circular (like a feature that relies on itself). Analyzing the structure of an argument, therefore, is essential to assess its soundness, just as testing reveals product reliability. Effective reasoning ensures the conclusion is a strong, logical consequence of the evidence presented, mirroring a successful product launch substantiated by extensive market research and testing. The strength of this connection is pivotal in logical analysis and directly parallels product functionality in its robustness and reliability.

How many logic gates are there?

Think of it like LEGOs: You have a limited set of basic bricks (AND, OR, NOT), yet you can build an incredibly diverse range of complex structures (all eight logic operations). This fundamental building block approach is crucial for designing efficient and scalable digital circuits.

Here’s a breakdown:

Basic Gates (the LEGO bricks):

AND: Outputs true only if ALL inputs are true.
OR: Outputs true if AT LEAST ONE input is true.
NOT: Inverts the input (true becomes false, false becomes true).

Derived Gates (complex LEGO creations): These gates can be built using combinations of the basic three. Examples include:

NAND (NOT AND): The opposite of AND.
NOR (NOT OR): The opposite of OR.
XOR (Exclusive OR): True only if ONE input is true (not both).
XNOR (Exclusive NOR): The opposite of XOR.
IMPLIES: A conditional statement. (A implies B is only false if A is true and B is false).

Practical Implications: Understanding the relationship between these basic and derived gates is critical in digital circuit design, impacting factors like power consumption, speed, and overall circuit complexity. Different gates have varying performance characteristics, so selecting the right ones is crucial for optimization. Modern integrated circuits (ICs) often contain millions of these gates, demonstrating their importance in today’s technology.

What does an eye in a triangle mean?

The Eye in the Triangle, also known as the All-Seeing Eye or Radiant Delta, is a powerful symbol with a rich history. Primarily associated with Freemasonry, it represents the Great Architect of the Universe, a supreme being overseeing the lodge’s activities. This iconic image, depicting an eye enclosed within a triangle, originates from Catholic iconography, though its use within Masonry isn’t officially sanctioned. The triangle itself often symbolizes the Holy Trinity in Christian contexts, adding another layer of interpretation. The symbolism resonates with broader concepts of divine providence, omniscience, and the ever-watchful gaze of a higher power. Its enduring appeal lies in its ability to evoke a sense of both awe and mystery, prompting diverse interpretations across cultures and belief systems. Its presence on various products, from jewelry to clothing, reflects its enduring cultural significance and versatile aesthetic appeal. Interestingly, its adoption by conspiracy theorists has somewhat tainted its original meaning, creating a distinct contrast between its historical context and modern usage. This fascinating duality contributes to the symbol’s ongoing allure and its continued relevance in contemporary society.

What logic gates constitute the basic set?

The Logic Gate Trinity: Building Blocks of Digital Power

Digital circuits rely on a surprisingly small set of fundamental building blocks: the AND, OR, and NOT gates. Think of them as the atoms of the digital world. The AND gate (logical multiplication or conjunction) outputs a true signal only when *all* its inputs are true. The OR gate (logical addition or disjunction) outputs true if *at least one* input is true. Finally, the NOT gate (logical negation or inversion) simply flips the input: true becomes false, and vice versa.

These three seemingly simple gates are functionally complete. This means any conceivable logical operation, no matter how complex, can be constructed using only combinations of AND, OR, and NOT gates. This foundational trio underpins everything from simple light switches to the incredibly complex processors powering your smartphone – a testament to the elegance and power of Boolean algebra.

Beyond the Basics: Efficiency and Optimization

While functionally complete, using only AND, OR, and NOT gates for complex circuits can be inefficient. For practical reasons, digital circuit designers often utilize additional gates like NAND (NOT-AND) and NOR (NOT-OR) gates, which provide equivalent functionality but with simpler, more compact circuit implementations. These gates offer a balance between functionality and efficiency in modern digital design.

The Future of Logic: Exploring New Frontiers

While the fundamental trio remains cornerstone, research continues to explore novel logic gates and architectures for greater efficiency and speed in future computing technologies. This includes exploring quantum logic gates and other non-classical computing paradigms promising to revolutionize computing capabilities.

What are the four laws of logic?

OMG! Aristotle’s Laws of Thought are like the ultimate shopping guide for your brain! They’re the must-have items for clear thinking, totally essential for scoring amazing deals on logic!

Law of Identity: This is your “this is *exactly* what I ordered” law. A thing is identical to itself. Think of finding that perfect pair of shoes online – it’s *that* pair and *no other*.
Law of Non-Contradiction: No more buyer’s remorse! A statement can’t be both true and false at the same time. It’s either a total steal or a complete rip-off, no in-between.
Law of Excluded Middle: It’s either a sale or it’s not. There’s no third option! Super helpful for weeding out those misleading “almost-on-sale” prices.
Law of Sufficient Reason: No impulse buys! Every statement needs a good reason to exist. Think of it as needing a solid reason to add something to your cart – you need it or it’s not a justified purchase.

Pro Tip: Mastering these laws will help you avoid those impulse purchases and make sure you’re making rational decisions, both in shopping and in life. It’s like having a personal shopper for your mind, ensuring you only buy the best stuff!

These laws were developed because people needed a way to think clearly and make sound judgments – seriously important, whether choosing between designer handbags or life decisions!

What does the symbol ≡ mean?

The symbol ≡, in logic, represents logical equivalence. Think of it like a super-powered equals sign for your Boolean circuits – the digital heart of your gadgets. It means two statements have the same truth value; they’re either both true or both false. This is crucial in programming and digital design. For example, in a smart home system, the statement “Temperature is above 25°C” might be logically equivalent to “Air conditioning is switched on.” If one is true, the other must also be true, and vice-versa. This equivalence allows the system to function seamlessly, automating actions based on interconnected conditions. The symbol ↔ is often used interchangeably, emphasizing the bidirectional nature of this relationship. This underlying logic powers everything from your phone’s auto-correct to complex algorithms in AI, ensuring devices respond as intended based on consistent truth values. Understanding logical equivalence is a key to appreciating the sophisticated systems driving our modern tech.

This concept isn’t limited to simple on/off scenarios. Imagine complex conditions in a self-driving car. “Car is approaching an intersection AND traffic light is red” might be equivalent to “Car should brake.” The ≡ symbol ensures the system correctly interprets this combination of conditions, guaranteeing safety. This is why logical equivalence is not just a theoretical concept – it’s the backbone of dependable, efficient, and safe gadgetry.

The practical implications extend beyond automated systems. Debugging code often involves checking for logical equivalence between expected and actual program behavior. Understanding this concept helps developers identify and fix errors, leading to smoother, more reliable software for your apps and games.

What are the basic logic gates in a computer?

At the heart of every computer lies a surprisingly simple secret: logic gates. These tiny electronic circuits, the fundamental building blocks of computation, perform basic logical operations. The core gates are AND, OR, NOT, NAND (NOT-AND), and NOR (NOT-OR). Think of them as the brain cells of your computer, each making incredibly fast decisions based on simple rules.

But how do these few simple gates achieve the complexity of modern computing? The magic lies in their combinability. Like LEGO bricks, you can connect these gates in countless configurations to create more complex logic functions. Any digital circuit, no matter how sophisticated, can be ultimately broken down into a network of these basic gates. This principle is the foundation of digital design.

Beyond the core gates, another crucial component is the flip-flop (also known as a trigger). Unlike the other gates that operate purely on their inputs, flip-flops have memory. They can store a single bit of information – a 0 or a 1 – and hold it until instructed to change. This memory capability is essential for storing data and instructions, forming the basis of computer memory and registers.

Key Characteristics of Logic Gates:

Inputs and Outputs: Typically, gates have multiple inputs (two to eight are common) and one or two outputs.
Speed: These operations happen incredibly fast, often measured in nanoseconds or even picoseconds.
Boolean Algebra: The behavior of these gates is formally described using Boolean algebra, a mathematical system that uses binary values (0 and 1) to represent true and false.

Understanding the Core Gates:

AND Gate: Outputs true (1) only if all inputs are true (1).
OR Gate: Outputs true (1) if at least one input is true (1).
NOT Gate (Inverter): Reverses the input; true (1) becomes false (0), and vice versa.
NAND Gate: The opposite of an AND gate; outputs false (0) only if all inputs are true (1).
NOR Gate: The opposite of an OR gate; outputs true (1) only if all inputs are false (0).

From simple calculations to running complex software, every computer operation ultimately relies on the precise and incredibly fast switching of these fundamental logic gates. Their seemingly simple nature belies their immense power and importance in the world of modern computing.

What are the basic logic elements of a computer?

OMG! You wouldn’t BELIEVE the amazing building blocks of a computer! They’re called logic gates – think of them as the ultimate fashion accessories for your tech wardrobe! We’ve got the AND gate, the OR gate, and the NOT gate – they’re like the classic little black dresses of digital circuitry, totally essential. Then there are the more exclusive, super-trendy options: the NAND (AND-NOT) and NOR (OR-NOT) gates – seriously, every computer *needs* these to be truly fabulous!

And the pièce de résistance? The flip-flop (or trigger)! This isn’t just *any* accessory; this is the ultimate statement piece – a memory cell that holds onto data like a VIP handbag holds your essentials. It’s seriously stylish and crucial for computer memory.

Seriously, with just these few basic gates, you can create ANY logical function! It’s like having a whole wardrobe of designer clothes, all built from just a few basic patterns. The possibilities are endless! They’re the foundation of every single digital circuit. You can build anything from simple adders to complex microprocessors with them! It’s so cool!

What types of logic are there?

Logic comes in different flavors, like choosing from a wide selection of online products! There’s Formal Logic, your basic, no-frills, reliable model – it analyzes the structure of arguments, ensuring they’re airtight. Think of it as the classic white t-shirt of logical reasoning – always in style and essential for building a solid foundation.

Then we have Dialectical Logic – this one’s more dynamic, exploring the evolution of ideas through contradiction and synthesis. It’s like that trendy new gadget everyone’s talking about – a bit more complex but incredibly powerful for understanding change and progress.

And finally, there’s Mathematical Logic, the high-tech, premium option. It uses mathematical symbols and methods to analyze arguments, offering a level of precision formal logic can only dream of. It’s your top-of-the-line, feature-rich option for serious logical analysis, but might require a steeper learning curve.

Formal logic focuses on reasoning itself. It’s less about what you’re reasoning *about* and more about how well you’re doing it. This makes it a critical tool across various fields, offering a universal standard for rigorous thinking, and enhancing problem-solving skills.

What logical operations are there?

There are three fundamental logical operations: conjunction (logical AND, denoted as ∧, *, or sometimes implicitly), disjunction (logical OR, denoted as ∨ or +), and inversion (logical NOT, denoted as ¬ or a bar over the logical variable).

Think of conjunction as requiring *all* conditions to be true for the overall result to be true. For example, a smart home system might only activate its security system (output) if both the door sensor (input A) AND the window sensor (input B) detect intrusion (A ∧ B = true). If either sensor fails to detect intrusion, the system remains inactive.

Disjunction, conversely, requires *at least one* condition to be true. Imagine a sprinkler system activating if it either senses low soil moisture (input A) OR the timer (input B) indicates it’s time to water (A ∨ B = true). The system activates even if only one of these conditions is met.

Inversion simply reverses the truth value of a statement. A smoke detector’s alarm (output) is activated (true) if the smoke sensor (input A) detects smoke (A = true), otherwise the alarm remains inactive (¬A = false). In essence, it’s a simple ‘yes’ or ‘no’ flip.

These three operations, while seemingly simple, form the building blocks for all complex logical expressions. Understanding their behavior is crucial for anyone working with Boolean logic, digital circuits, programming, or any field involving decision-making based on conditional statements.

Which logic gates are considered fundamental?

As a regular buyer of logic gates, I know the three fundamental logic operations are:

AND (Conjunction): Represented by ∧, *, or sometimes nothing at all. Think of it like this: the output is only TRUE if *both* inputs are TRUE. It’s like needing two keys to open a door – you need both to succeed. Many applications use it for filtering data, only allowing passage if multiple conditions are met.
OR (Disjunction): Represented by ∨ or +. This is the “either/or” scenario. The output is TRUE if *at least one* input is TRUE. It’s like having two paths to a destination; if you can use either path, you’ll get there. Often used in decision-making processes where several triggers might trigger an action.
NOT (Inversion/Negation): Represented by ¬ or a bar over the variable. It simply flips the input. TRUE becomes FALSE, and FALSE becomes TRUE. It’s the ultimate toggle switch, essential for creating complex logic from simpler building blocks. Essential for creating inverters, which are used everywhere from memory to control circuits.

While these three are fundamental, it’s worth noting that all other logic gates can be built using combinations of these three. This is crucial for circuit miniaturization – by focusing on these basics, manufacturers can create incredibly complex systems using very simple components.

What does & mean in Boolean algebra?

In Boolean algebra, the ampersand (&) represents the logical AND operation, also known as conjunction or logical multiplication. It’s often symbolized by an asterisk (*) or a dot (.). This operation returns true only if both inputs are true; otherwise, it returns false.

To illustrate, consider these examples:

True & True = True
True & False = False
False & True = False
False & False = False

This is fundamentally different from the logical OR operation (often represented by a plus sign (+) or a forward slash (/)), which returns true if at least one input is true. The logical NOT operation (often symbolized by a bar over the expression) inverts the input value; true becomes false and vice versa.

Practical Application & Testing: Understanding these logical operations is crucial in software testing. Think of test cases where you need to verify multiple conditions simultaneously. For instance, a successful login might require both a valid username and a correct password. The AND operation perfectly models this scenario, allowing testers to create robust and precise test cases. Similarly, OR operations are useful when checking for alternative success conditions, and NOT operations are used to check for failure conditions.

Testing Strategies: Effective testing often involves constructing truth tables, systematically evaluating all possible combinations of input values. This exhaustive approach helps ensure thorough coverage and minimizes the risk of overlooked bugs. Tools like test management software can aid in this process, enabling efficient tracking and reporting of test results.

Equivalence Partitioning: Divide inputs into groups that are expected to behave similarly. This helps to reduce the number of test cases while maintaining good coverage.
Boundary Value Analysis: Focus on values at the edges of input ranges, as these are more likely to uncover defects.
Decision Table Testing: Especially useful for complex scenarios involving multiple conditions and actions, visually representing all possible combinations and their outcomes.

How does a 2-input NAND gate work?

The NOT gate, also known as an inverter, is a fundamental building block in digital logic. It’s incredibly simple: one input, one output. Its function is to invert the logic level. A low input produces a high output, and vice-versa. This seemingly basic operation is crucial for manipulating and controlling digital signals.

Key Features: Think of it as a digital switch that flips the state. A 0 becomes a 1, and a 1 becomes a 0. This inversion is essential for creating more complex logic functions.

Applications: Beyond its standalone use, the NOT gate forms the basis of many other logic gates like NAND, NOR, and XOR gates, all essential for constructing processors, memory, and countless other digital devices. Its simplicity and reliability make it a workhorse of digital electronics.

Technical Specifications: While the logic function is binary (0 or 1), real-world implementations will have specific voltage thresholds defining the “high” and “low” levels. These thresholds are crucial to consider for compatibility with other digital components.

Variations: Though the basic principle is consistent, NOT gates can be implemented using various technologies—transistors, integrated circuits, and even optical components—each with its own advantages in terms of speed, power consumption, and size.

What does the symbol z mean?

The symbol “Z” has emerged as a potent symbol of support for the Russian military operation in Ukraine. Initially appearing in pro-war social media posts, it quickly gained traction, becoming a ubiquitous feature in patriotic flash mobs and displayed prominently on vehicles and clothing.

Meaning and Significance: While the official meaning is “Za Pobedu” (For Victory), its adoption has transcended simple slogan status. The “Z” has become a readily identifiable marker of pro-war sentiment, and its use often carries implications beyond simple support, indicating a level of fervent nationalism and alignment with the military’s goals.

Variations and Usage: Though “Z” is the most common, related symbols like “V,” “O,” and “A” also appear, often in conjunction, forming a sort of visual code. The specific meanings of these variations are less clear, but they collectively contribute to the symbol’s overall message.

Impact and Controversy: The widespread use of the “Z” symbol has sparked considerable controversy. It has become increasingly associated with aggressive rhetoric and militarism, and its public display has been criticized by many as a propagandistic tool. Its appearance on civilian objects contributes to the normalization of the conflict and the associated narratives within Russian society.

Visual Appeal: The symbol’s simple, bold design contributes to its widespread appeal and ease of reproduction.
Adaptability: Its versatility allows for adaptation across various media and platforms.
Controversy and Backlash: The symbol has generated significant international criticism and has become a sensitive point in the international debate surrounding the conflict.
The “Z” symbol’s rise showcases the power of simple symbols in shaping public opinion and mobilizing support for political causes.
Its widespread adoption underlines the importance of understanding visual communication and its role in propaganda.
The controversy surrounding the “Z” highlights the complex interplay between nationalism, patriotism, and the impact of armed conflict on civilian life.

What are the logical operators?

Logical operators are the backbone of any conditional statement, determining program flow based on truth values (true or false).

Understanding the Operators:

Unary NOT (!): This operator inverts the truth value of a single operand. Think of it as a light switch – !true becomes false, and !false becomes true. Testing this is straightforward: simply set up boolean variables and observe the output. Pay close attention to how it interacts with complex expressions for accurate results.
Binary AND (&&, &): Both operands must be true for the entire expression to be true. Imagine two switches in series; both must be “on” for the light to work. In testing, ensure you cover all four combinations of true/false input to confirm correct behavior. Consider edge cases where one operand might unexpectedly evaluate to false.
Binary OR (||, |): If at least one operand is true, the entire expression is true. Think of two switches in parallel – the light turns on if either switch is “on”. Thorough testing should include all four truth value combinations, similar to AND. Note any differences between the bitwise OR (&) and logical OR (||) during your tests.
Binary XOR (^): This is the exclusive OR. The expression is true if *only one* operand is true. It’s like a light that switches on when one, but not both, switches are flipped. Testing should focus on the unique nature of this operator to ensure it functions exactly as expected.

Important Considerations for Testing:

Truth Tables: Use truth tables to systematically test all possible input combinations for each operator. This guarantees comprehensive coverage.
Edge Cases: Consider null or undefined values as inputs. How does the operator handle these scenarios? This is crucial for robustness.
Short-Circuiting: Understand how short-circuiting works with && and ||. If the first operand determines the overall result, the second operand might not be evaluated, potentially impacting performance or side-effects. Test this behavior explicitly.
Operator Precedence: Be aware of operator precedence and use parentheses to enforce the desired order of operations, especially in complex expressions. Test different grouping strategies to confirm correctness.

Different languages might have slight variations in syntax or behavior, so always consult the relevant documentation for the language you are using.

What logical units comprise a computer?

So, you’re asking about the logic components of a computer? Think of it like this: it’s built from fundamental building blocks, kind of like LEGOs, but way more complex. Every computer, regardless of brand (I’m a big fan of the latest Ryzen chips, by the way!), has these key parts:

First, you have memory (RAM, everyone knows that!), which is like a giant set of numbered boxes. Each box holds a tiny piece of information. The more boxes you have (measured in gigabytes, naturally), the more stuff your computer can juggle at once. Faster RAM means snappier performance; it’s a crucial upgrade if you’re into gaming or video editing.

Next, the processor (the CPU, the brain of the operation). This is split into two main sections: the control unit (CU), which is like the foreman, directing all the actions, and the arithmetic logic unit (ALU), which does the actual calculations and logical comparisons. The clock speed (measured in GHz) determines how fast it works – higher clock speeds mean more operations per second. And, of course, the number of cores impacts multitasking capabilities significantly; more cores mean smoother performance when running multiple applications simultaneously. I recently upgraded to a 12-core processor, and the difference is amazing!

Finally, there’s the input device – your keyboard, mouse, touchscreen, etc. – this is how you interact with the computer, providing it with instructions and data. And don’t forget the output devices (monitors, printers) which display or record the results. Although not explicitly mentioned in your question, they are crucial parts of the complete picture.

What are the basic elements of Boolean algebra?

Key Elements of Boolean Algebra: Your Ultimate Shopping Guide

Statements (Propositions): Think of these as the basic building blocks, like individual items in your online cart. Each statement holds a truth value – either true or false. Consider them the fundamental ‘products’ in our logical system.

Logical Operations (Operators): These are your essential shopping tools! They combine statements, just like you combine items in your cart. Key operators include AND, OR, and NOT (negation), each with unique functionalities mirroring different shopping actions.

Truth Tables: Your ultimate product comparison tool! Truth tables visually represent the output of logical operations based on all possible input combinations. Quickly see the results of applying logical operators – a must-have for efficient logical shopping!

Properties of Logical Operations: Understanding these is like knowing the store’s return policy. Commutative, associative, distributive laws, and De Morgan’s laws are your guarantees for consistent and reliable logical outcomes. Knowing these properties helps you optimize your logical ‘shopping’ experience.

Logical Elements (Gates): These are the physical implementations, like the store’s checkout system. They process logical operations in digital circuits – the engine behind all your online transactions.